Diving into Merkle Trees
This is a transcript of my talk on Diving into Merkle Trees that I will give
at Lambda Days and ScaleConf Colombia. Slides and video should be up soon!

Introduced in 1979 by Ralph C. Merkle in his Thesis: Secrecy, Authentications, and Public Key Systems, the Merkle Tree, also known as a binary hash tree, is a data structure used for efficiently summarizing and verifying the integrity of large sets of data enabling users to verify the authenticity of their received responses.
“The general idea in the new system is to use an
infinite tree of one-time signatures. […] Each node of the tree performs three
functions: (1) it authenticates the left sub-node (2) it authenticates the right
sub-node (3) it signs a single message.”
Initially, it was used for the purpose of one-time signatures and authenticated public key distribution, namely providing authenticated responses as to the validity of a certificate.

Ralph C. Merkle described a new digital signature that was able to sign an unlimited number of messages and the signature size would increase logarithmically as a function of the number of messages signed.
At this point we can identify the two main purposes of a Merkle Tree: (1) summarize large sets of data and (2) verify that a specific piece of data belongs to a larger data set.
One-Way Hashing Functions
Before diving into one-time signatures lets first get confortable with one-way functions. Usually, a one-way function is a mathematical algorithm that take inputs and provide unique outputs such as MD5, SHA-3, or SHA-256.
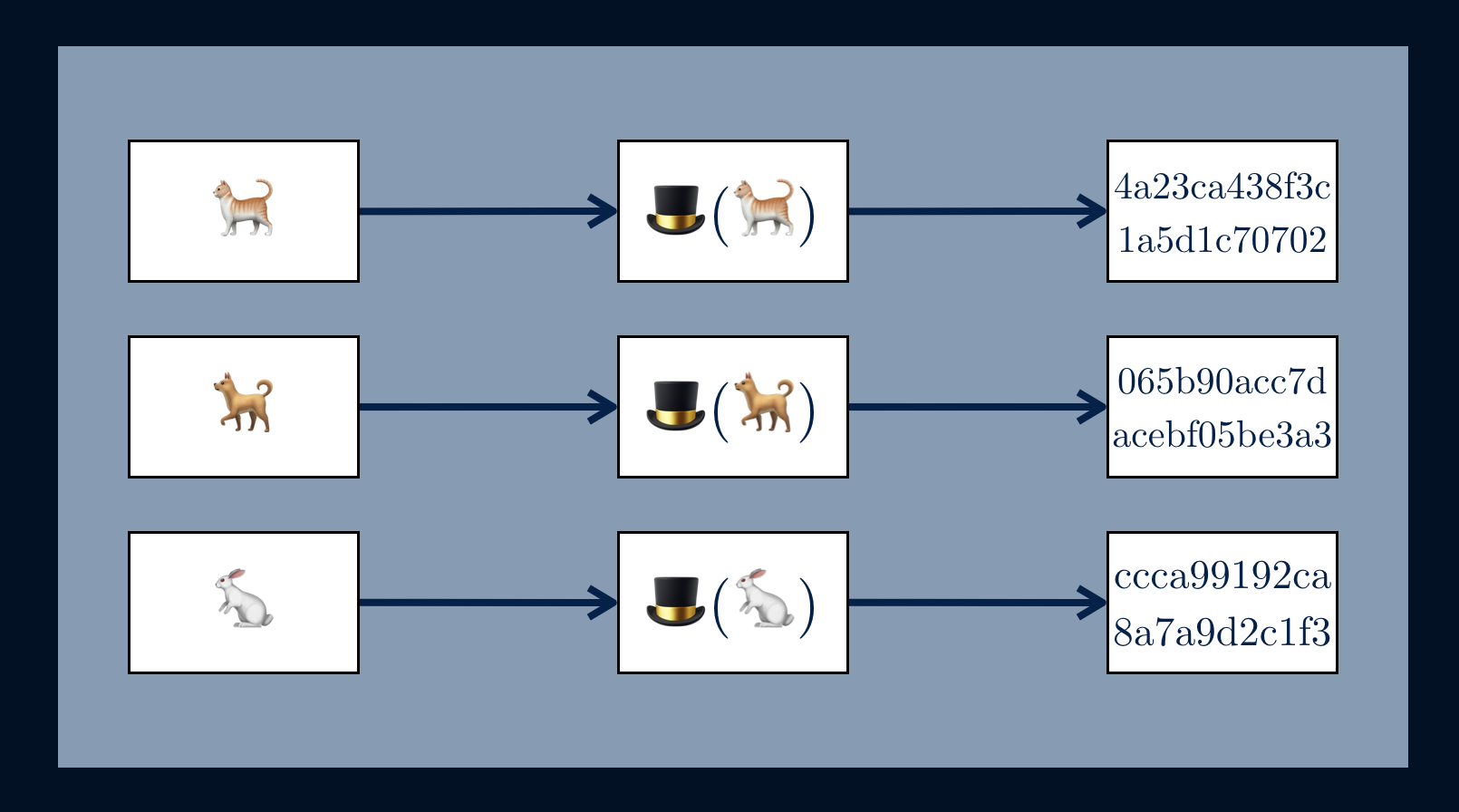
A one-way function F is a function that is
easy to compute, but difficult to invert. Given x and F, it is easy to
compute y=F(x), but given y and F, it is effectively impossible to compute
x.
One-way hashing functions are especially useful within Merkle Trees for two obvious reasons; storage and privacy.
With systems that contain massive amounts of data, the benefits of being able to store and identify data with a fixed length output can create vast storage savings and help to increase efficiency.
The person who computes y=F(x) is the only person who knows x. If y is publicly revealed, only the originator of y knows x, and can choose to reveal or conceal x at his whim!
One-time Signatures
Also in 1979, Leslie Lamport published his concept of One-time Signatures. Most signature schemes rely in part on one-way functions, typically hash functions, for their security proofs. The beauty of Lamport scheme was that this signature was only relying on the security of these one-way functions!
One time signatures are practical between a single pair
of users who are willing to exchange the large amount of data necessary but they
are not practical for most applications without further refinements.
If 1000 messages are to be signed before new public
authentication data is needed, over 20,000,000 bits or 2.5 megabytes must be
stored as public information.
If B had to keep 2.5 megabytes of data for 1000 other users, B would have to store 2.5 gigabytes of data. With further increases in the number of users, or in the number of message each user wants to be able to sign, the system would eventually become burdensome.
Improving One-time Signatures
Merkle focused on how to eliminate the huge storage requirements in the Lamport method and proposed an improved One-time Signature that reduced the size of signed messages by almost a factor of 2.
This improved method was easy to implement and cutted the size of the signed
message almost in half, although this was still too large for most applications;
instead of storing 2.5 gigabytes of data, B only had to store 1.25 gigabytes.

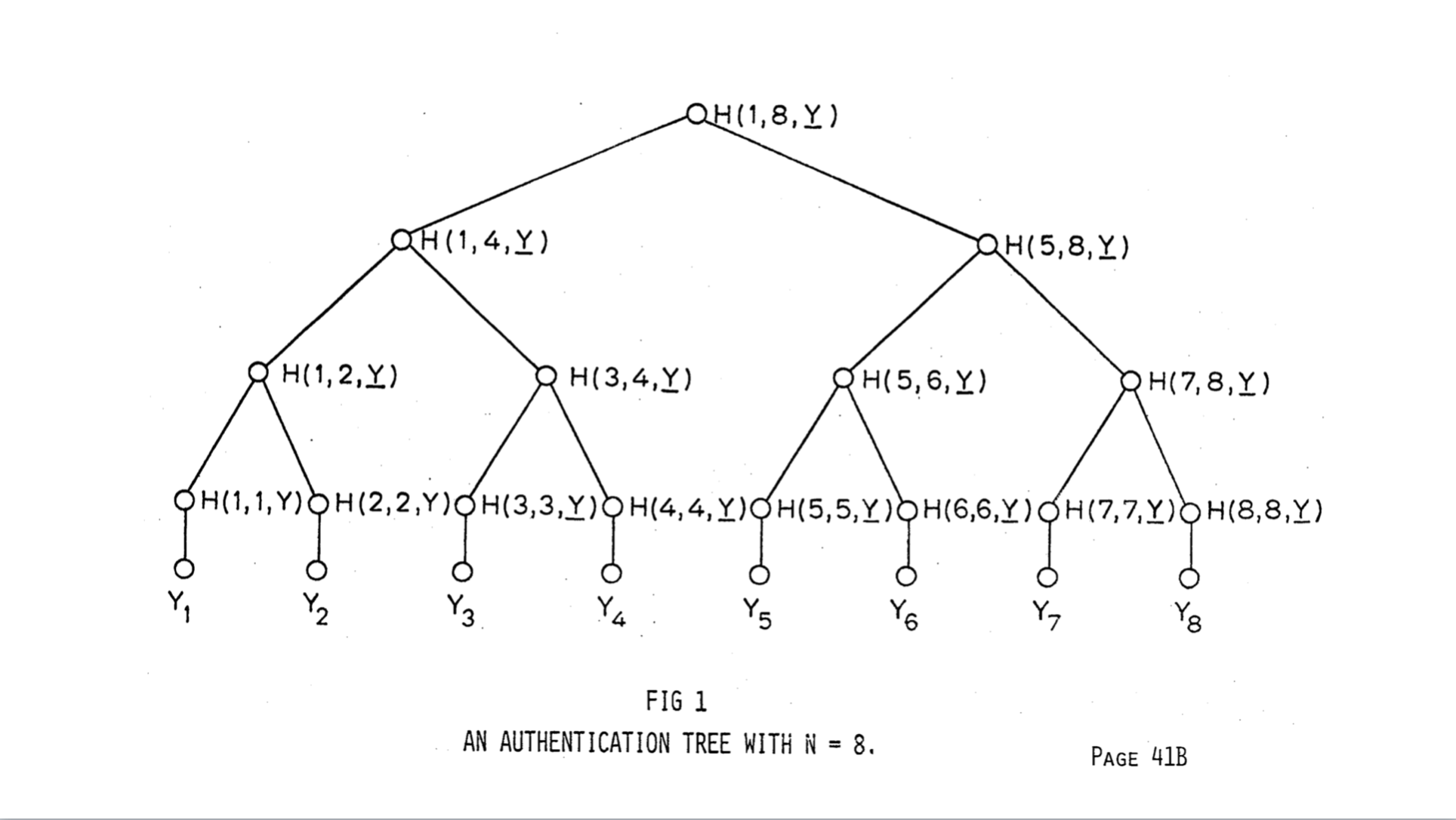
The method is called tree authentication because it’s computation forms a binary
tree of recursive calls. Using this method, requires only log2 n
transmissions. A close look at the algorithm will reveal that half the
transmissions are redundant since we’re able to compute a given parent node A
from their children A1 and A2, so there’s really no need to send A.
How to compute a Merkle Root?
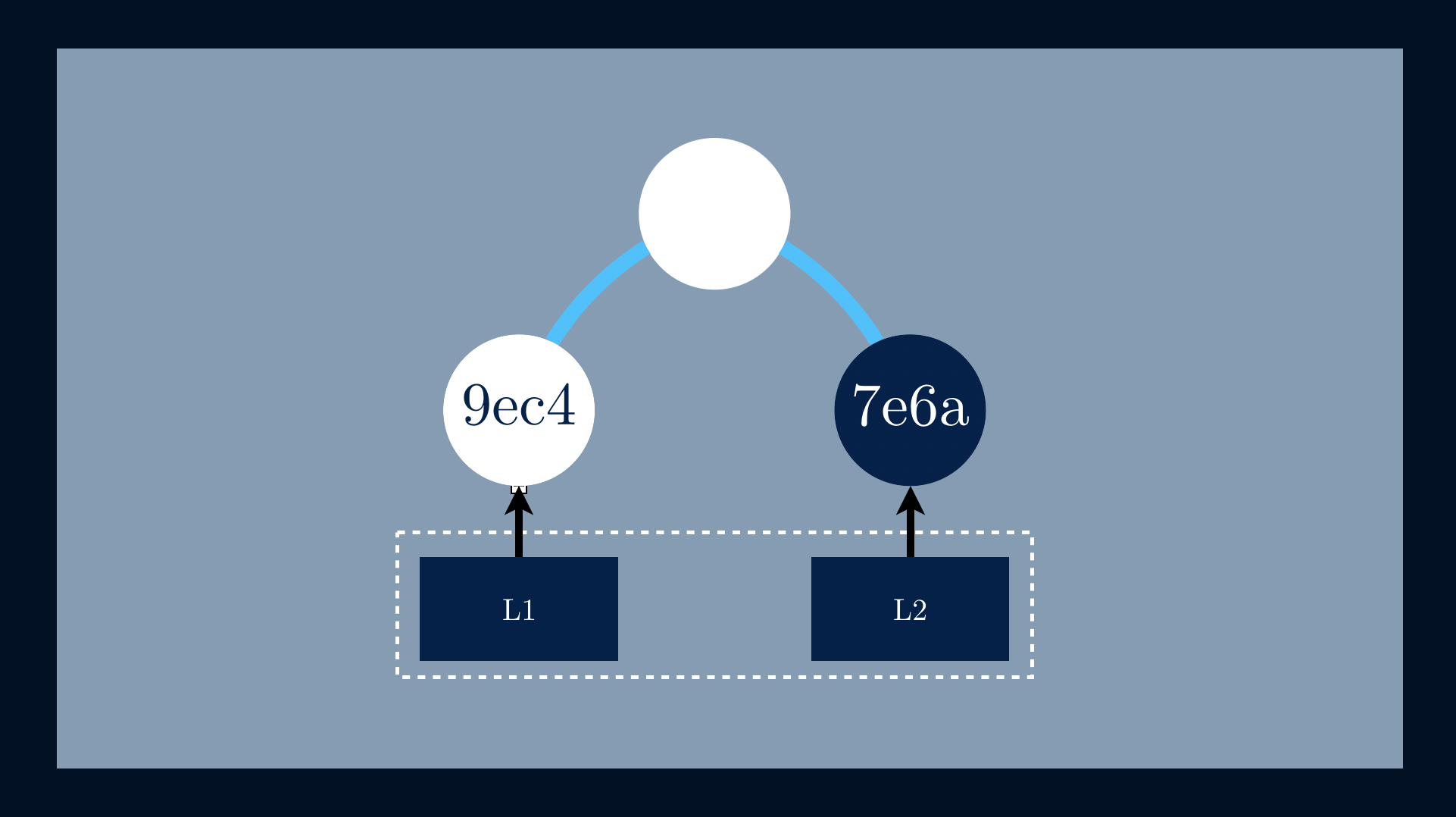
Given that we have a data file represented by a set of blocks [L1, L2].
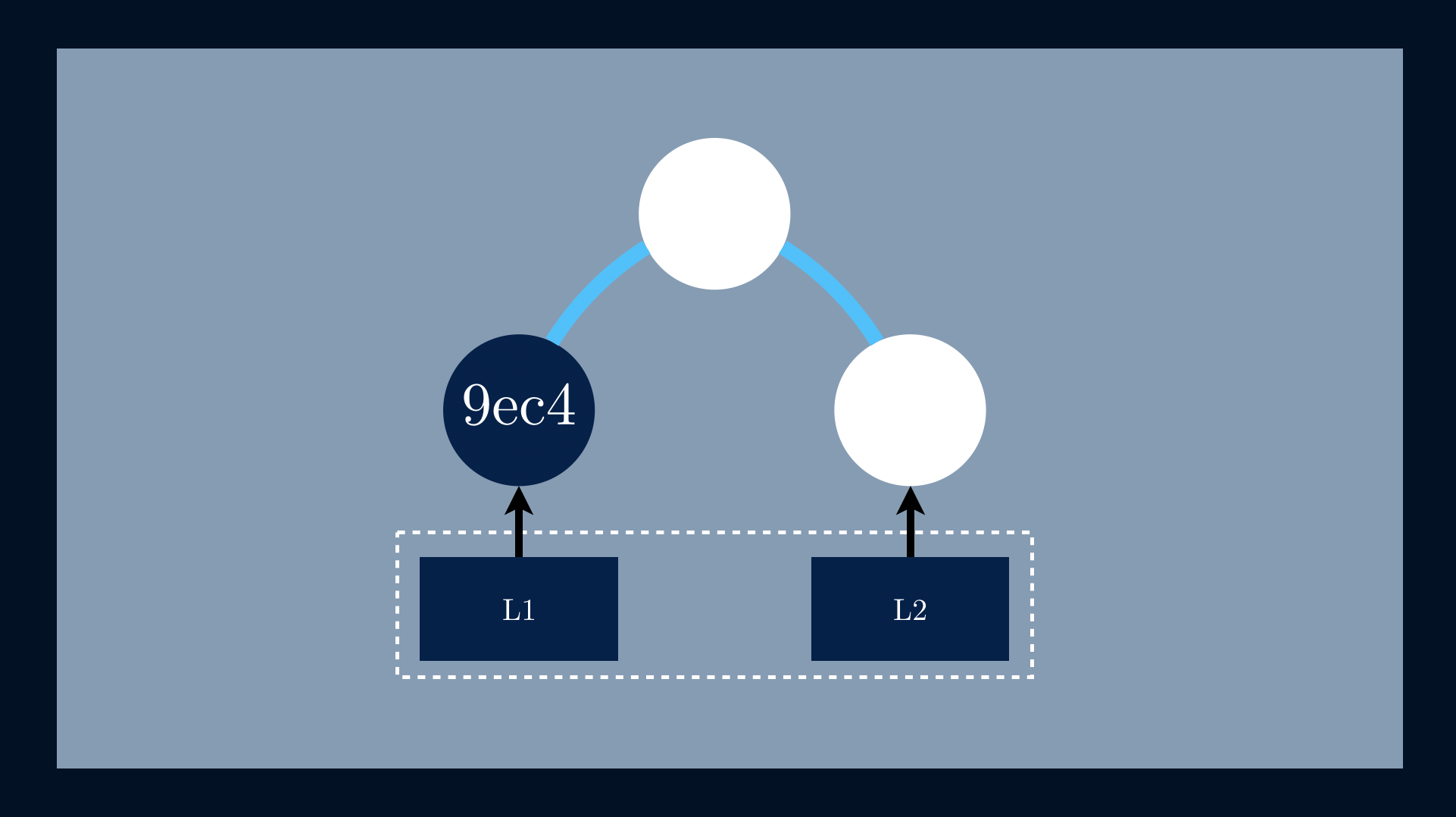
We start by applying a one-way hashing function to L1, h(📄L1) = 9ec4.
The next step is to apply the same function to L2, h(📄L2) = 7e6a.
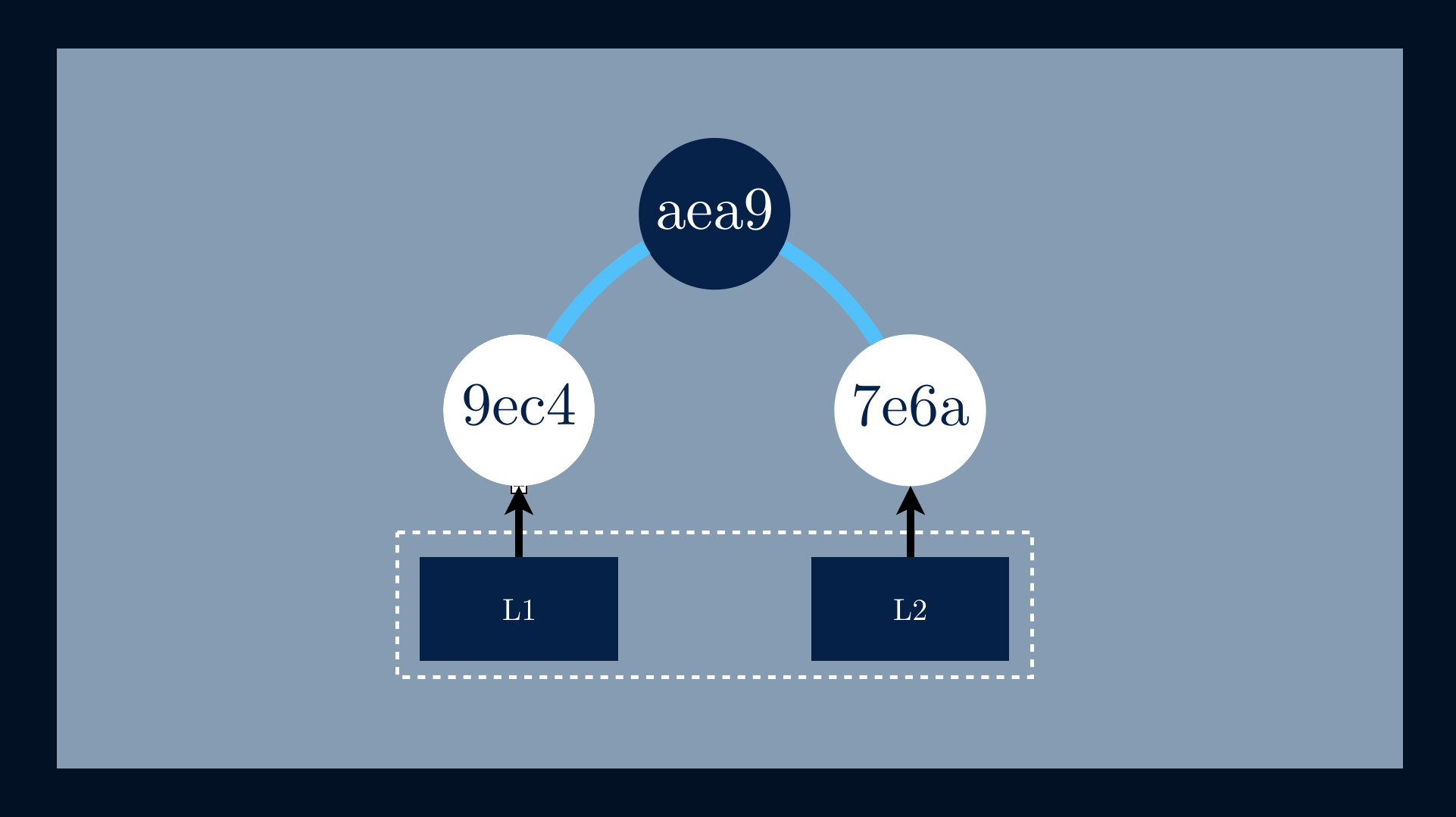
To calculate the parent node, we need always to concatenate both child hashes
h(📄L1) and h(📄L2) before applying, once again, the one-way hashing
function, h(h(📄L1) || h(📄L2)) = aea9.
At this point we know the building blocks of a Merkle Tree; let’s represent it in Elixir.
Building a Merkle-Tree
In order to build a Merkle Tree, we need to define three new types: Leaf,
Node, and the MerkleTree itself. Let’s start by defining Leaf – it
should contain the hash and the value of a given data block.
defmodule MerkleTree.Leaf do
defstruct [:hash, :value]
@type hash :: String.t
@type value :: String.t
@type t :: %MerkleTree.Leaf{
hash: hash,
value: value
}
end
The next type is Node – it should contain the left and right child
nodes, and the hash value of the concatenation of both child hashes.
defmodule MerkleTree.Node do
defstruct [:hash, :left, :right]
@type hash :: String.t
@type left :: MerkleTree.Node.t | MerkleTree.Leaf.t
@type right :: MerkleTree.Node.t | MerkleTree.Leaf.t
@type t :: %MerkleTree.Node{
hash: hash,
left: left,
right: right
}
end
And, finally, the Merkle Tree itself.
defmodule MerkleTree do
defstruct [:root]
@type root :: MerkleTree.Node.t
@type t :: %MerkleTree{
root: root
}
end
Hashing the data blocks
The first step to build a Merkle Tree is to hash the data blocks and
converting them to leaves. In order to hash something we need to define a new
module Crypto with a single function hash that should accept an input and is
responsible for encoding it using the appropriate one-way hashing function.
defmodule MerkleTree.Crypto do
def hash(input, type \\ :sha256) do
type
|> :crypto.hash("#{input}")
|> Base.encode16
end
end
Having blocks = ["L1", "L2", "L3", "L4"], the expected output would be:
[
%MerkleTree.Leaf{
value: "L1",
hash: "DFFE8596427FC50E8F64654A609AF134D45552F18BBECEF90B31135A9E7ACAA0"
},
%MerkleTree.Leaf{
value: "L2",
hash: "D76354D8457898445BB69E0DC0DC95FB74CC3CF334F8C1859162A16AD0041F8D"
},
%MerkleTree.Leaf{
value: "L3",
hash: "842983DE8FB1D277A3FAD5C8295C7A14317C458718A10C5A35B23E7F992A5C80"
},
%MerkleTree.Leaf{
value: "L4",
hash: "4A5A97C6433C4C062457E9335709D57493E75527809D8A9586C141E591AC9F2C"
}
]
By defining a function new that accepts blocks, we should be able to hash
the data blocks and convert them into Leafs.
defmodule MerkleTree do
alias MerkleTree.Leaf
alias MerkleTree.Crypto
def new(blocks) do
blocks
|> Enum.map(&%Leaf.build(&1, Crypto.hash(&1)))
end
end
Where Leaf.build/2 is just:
defmodule MerkleTree.Leaf do
def build(value, hash) do
%Leaf{value: value, hash: hash}
end
end
Calling the function above MerkleTree.new ["L1", "L2", "L3", "L4"] should
yield the expected output. Although, we’re not done yet.
Hashing the nodes
Remember that for creating a Node we need to join both child hashes and
apply the one-way hashing function once again?
defmodule MerkleTree.Node do
alias MerkleTree.Crypto
def new(nodes) do
nodes
|> Enum.map_join(&(&1.hash))
|> Crypto.hash
|> build(nodes)
end
def build(hash, [left, right]) do
%Node{hash: hash, left: left, right: right}
end
end
That’s basically what new is doing before calling build(nodes). Once we
have the Node hash value, we’re ready to create a new Node with hash,
left, and right. As an example, by calling the function above with these two
leaves:
MerkleTree.Node.new([
%MerkleTree.Leaf{
value: "L1",
hash: "DFFE8596427FC50E8F64654A609AF134D45552F18BBECEF90B31135A9E7ACAA0"
},
%MerkleTree.Leaf{
value: "L2",
hash: "D76354D8457898445BB69E0DC0DC95FB74CC3CF334F8C1859162A16AD0041F8D"
}
])
Would yield the following Node:
%MerkleTree.Node{
hash: "8C569660D98A20D59DE10E134D81A8CE55D48DD71E21B8919F4AD5A9097A98C8",
left: %MerkleTree.Leaf{
value: "L1",
hash: "DFFE8596427FC50E8F64654A609AF134D45552F18BBECEF90B31135A9E7ACAA0"
},
right: %MerkleTree.Leaf{
value: "L2",
hash: "D76354D8457898445BB69E0DC0DC95FB74CC3CF334F8C1859162A16AD0041F8D"
}
}
All the way up
Having a way to build a Node from a pair of nodes, we can now make use of
recursion to calculate the remaining nodes up to the Merkle root. Let’s
complete the new function:
defmodule MerkleTree do
alias MerkleTree.Leaf
alias MerkleTree.Crypto
def new(blocks) do
blocks
|> Enum.map(&%Leaf.build(&1, Crypto.hash(&1)))
|> build
end
end
Currently, this new function it’s yielding a list of leaves. Let us define a
build function that accepts that list of leaf nodes with the goal of
grouping it into several pairs of leaf nodes in order to build the parent
Node by concatenating both left and right child hashes.
defp build(nodes) do
nodes
|> Enum.chunk_every(2)
|> Enum.map(&MerkleTree.Node.new(&1))
|> build
end
Note that we’re making use of tail recursion to build our Merkle Tree from the ground up to the root. Still, we need to stop that recursive processing.
defp build([root]) do
%MerkleTree{root: root.hash, tree: root}
end
defp build(nodes) do
nodes
|> Enum.chunk_every(2)
|> Enum.map(&MerkleTree.Node.new(&1))
|> build
end
By pattern matching a single element root in the list of nodes, we’re now able
to stop the processing and return a MerkleTree.
The final new function would look like this:
defmodule MerkleTree do
alias MerkleTree.Leaf
alias MerkleTree.Crypto
def new(blocks) do
blocks
|> Enum.map(&%Leaf.build(&1, Crypto.hash(&1)))
|> build
end
end
Finally, by calling the function MerkleTree.new ["L1", "L2", "L3", "L4"] would
yield the following result:
%MerkleTree{
root: "B8EC6582F5B8ED1CDE7712275C02C8E4CC0A2AC569A23F6B7738E6B69BF132E6",
tree: %MerkleTree.Node{
hash: "B8EC6582F5B8ED1CDE7712275C02C8E4CC0A2AC569A23F6B7738E6B69BF132E6",
left: %MerkleTree.Node{
hash: "8C569660D98A20D59DE10E134D81A8CE55D48DD71E21B8919F4AD5A9097A98C8",
left: %MerkleTree.Leaf{
value: "L1",
hash: "DFFE8596427FC50E8F64654A609AF134D45552F18BBECEF90B31135A9E7ACAA0"
},
right: %MerkleTree.Leaf{
value: "L2",
hash: "D76354D8457898445BB69E0DC0DC95FB74CC3CF334F8C1859162A16AD0041F8D"
}
},
right: %MerkleTree.Node{
hash: "29C5146A0AABBC4444D91087D91D2637D8EB4620A686CF6179CCD7A0BFB9B8EF",
left: %MerkleTree.Leaf{
value: "L3",
hash: "842983DE8FB1D277A3FAD5C8295C7A14317C458718A10C5A35B23E7F992A5C80"
},
right: %MerkleTree.Leaf{
value: "L4",
hash: "4A5A97C6433C4C062457E9335709D57493E75527809D8A9586C141E591AC9F2C"
}
}
}
}
Audit Proof
As we already know, we can use a Merkle Tree to verify that a specific piece of data belongs to a larger data set. The Merkle audit proof is the missing nodes required to compute all of the nodes between the data block and the Merkle root. If a Merkle audit proof fails to produce a root hash that matches the original Merkle root hash, it means that our data block is not present in the tree.
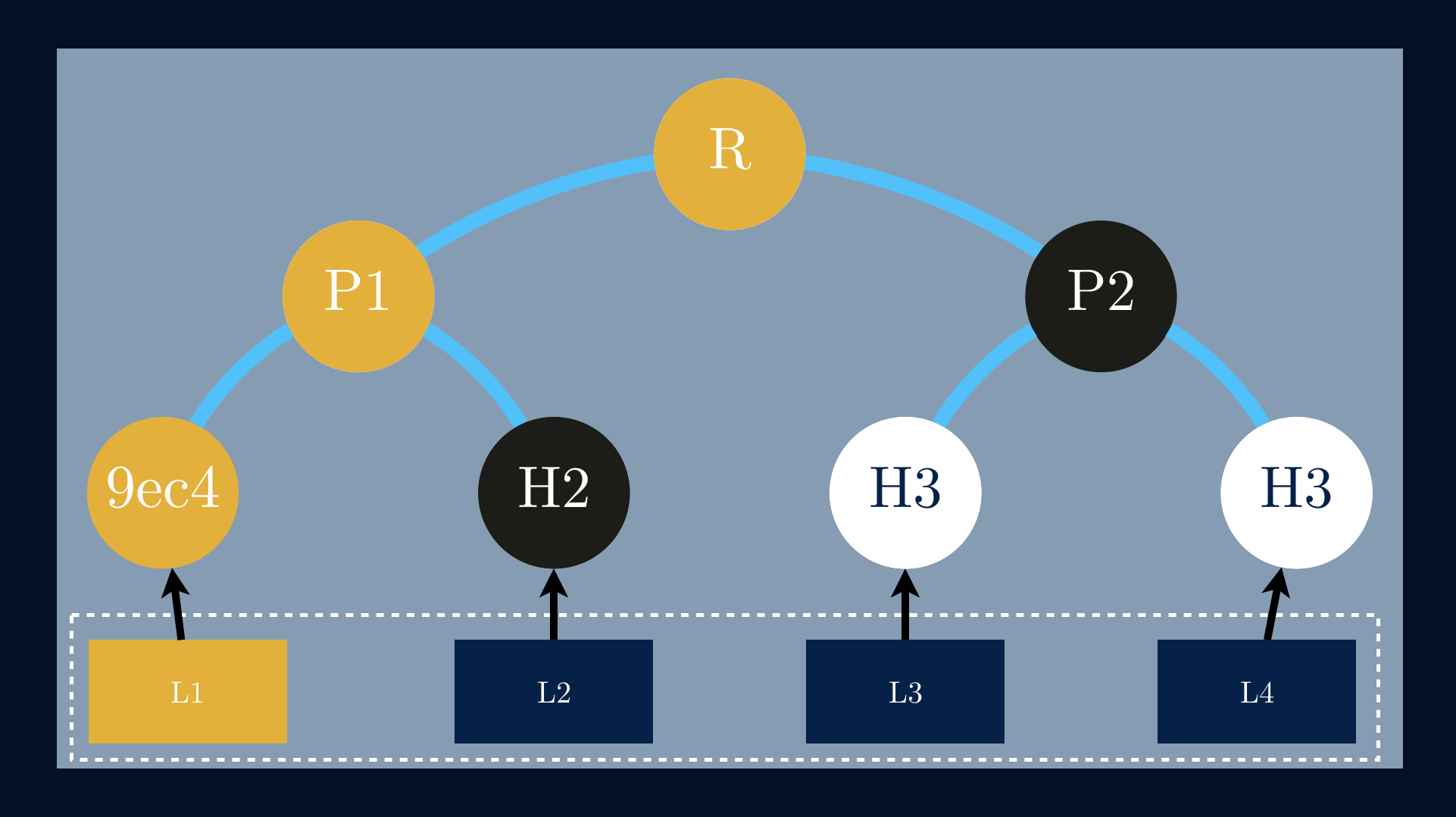
In this example, we need to provide a proof that the data block L1 exists in
the tree. Since we already know the hash value of L1, we’ll need the hash
value of L2 in order to compute P1. Now that we are able to compute P1 we
finally need to get P2 to compute R. In this specific case the Merkle audit
proof is a list of nodes [H2, P2].
The use of tree authentication is now fairly clear. A given user
A transmits R to another user B. A then transmits the authentication path for
Yi. B knows R, the root of the authentication tree, by prior arrangement. B can
then authenticate Yi, and can accept any Ynth from A as genuine.
How they are useful?
Merkle trees are especially useful in distributed, peer-to-peer systems where the same data should exist in multiple places. By using Merkle Trees we can detect inconsistencies between replicas, reduce the amount of transferred data enabling peer-to-peer file sharing, and maintaining several versions of the same tree, also called persistent data-structures.
Detect inconsistencies
Having a data file represented by a data structure we’re able to detect inconsistencies between replicas of that same tree. Take for example three replicas of the same Merkle Tree – just comparing the root nodes we can make sure that those trees are not the same, or in this case, there are inconsistencies between them.
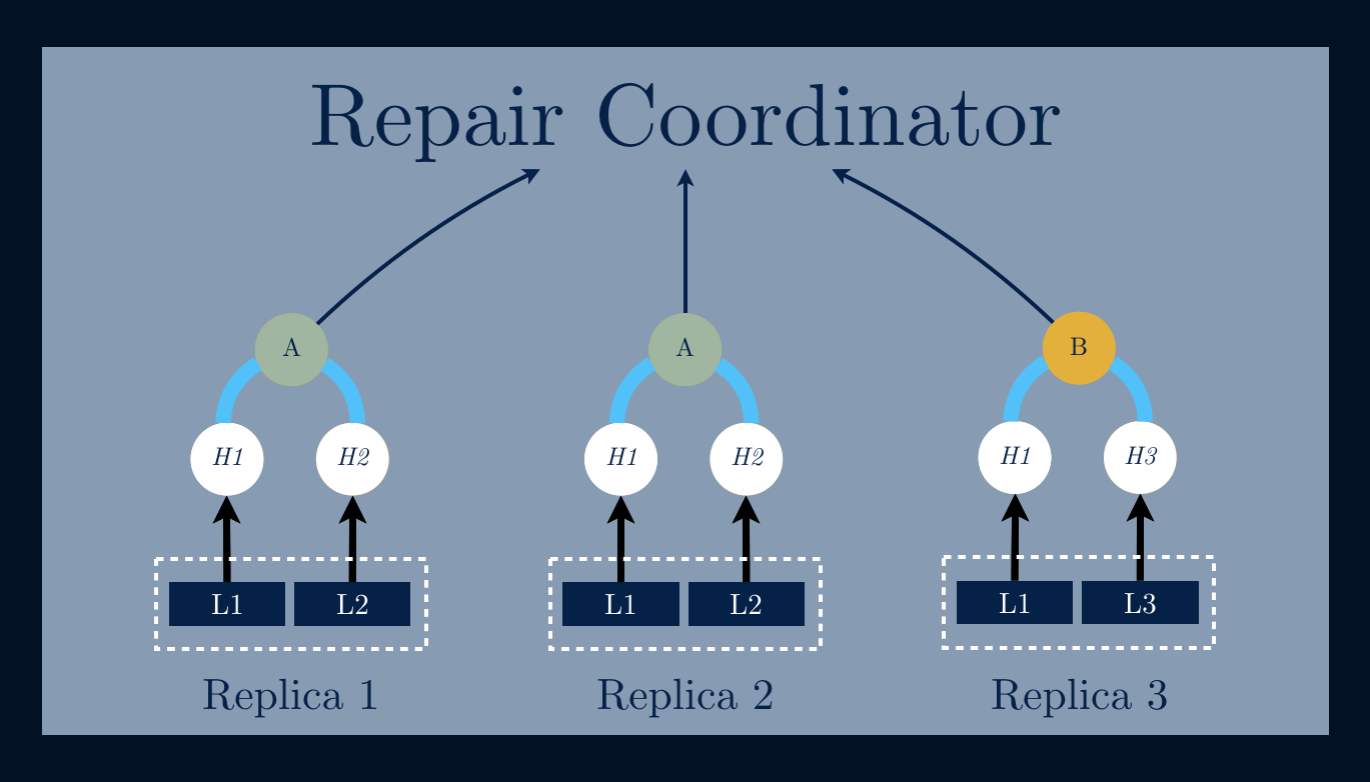
By using an Anti-entropy mechanism, we’re able to notice that both trees have inconsistent data and that triggers a process that copies only the data needed to repair the inconsistent tree.
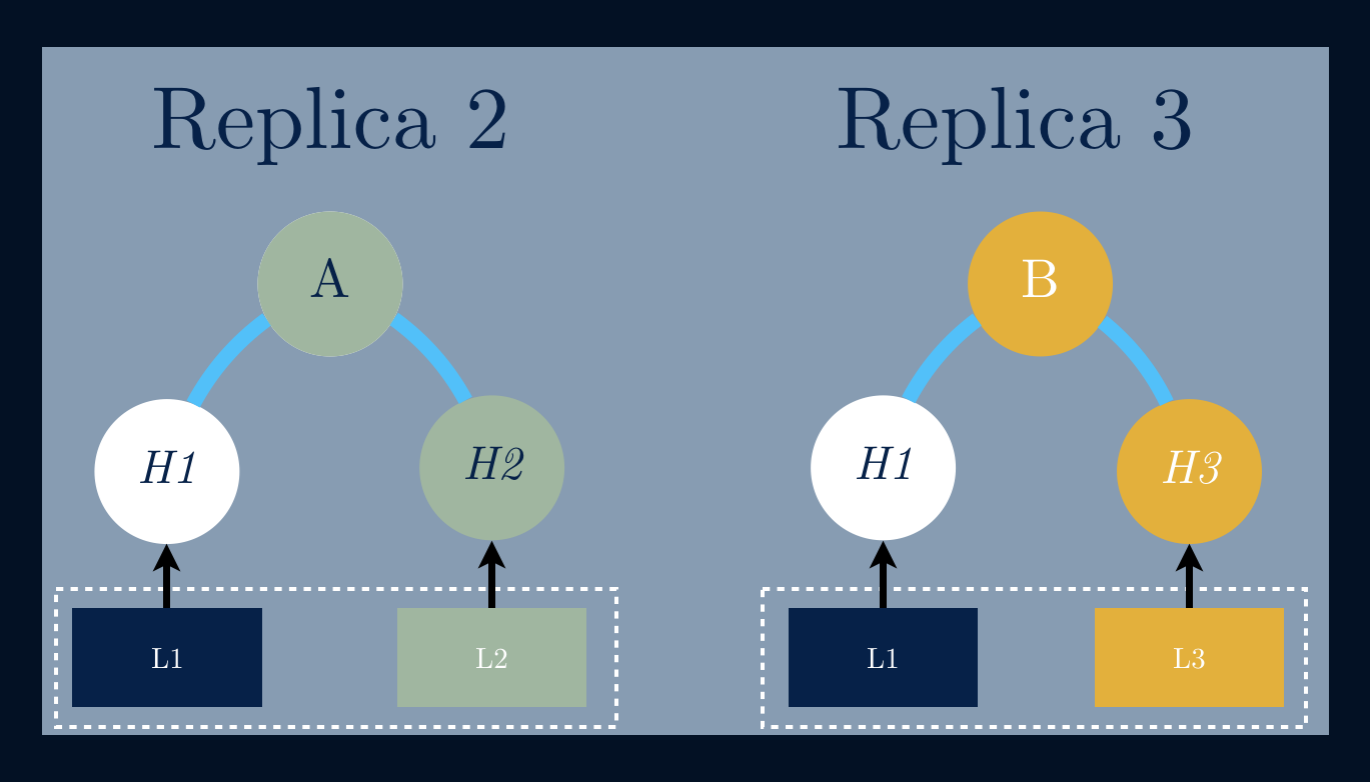
To compare the state of two nodes, they exchange the corresponding Merkle Trees by levels, only descending further down the tree if the corresponding hashes are different. If two corresponding leaf nodes have different hashes, then there are objects which must be repaired.
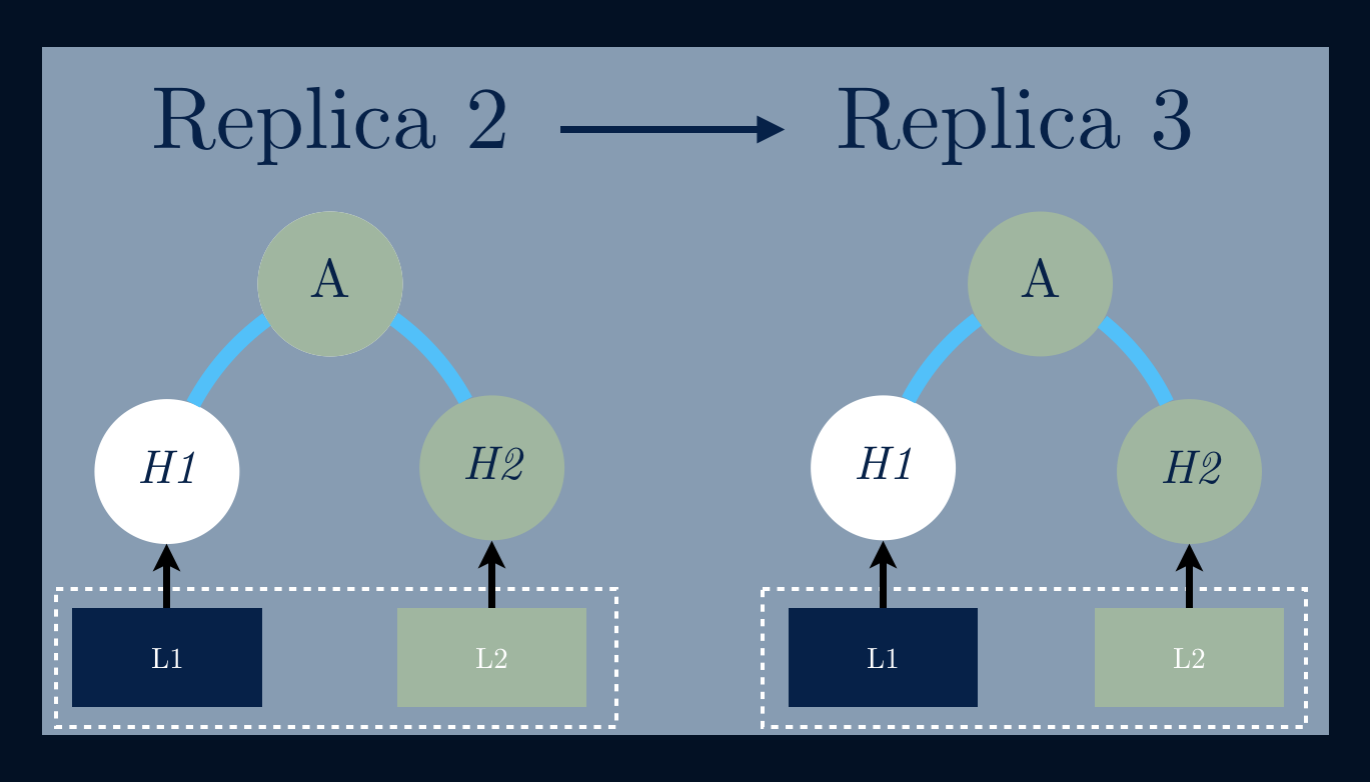
This is actually used by Dynamo, Riak, and Cassandra to repair bad replicas!
Peer-to-peer file sharing
The principal advantage of Merkle Trees is that each branch of the tree can be checked independently without requiring nodes to download the entire data set. This makes peer-to-peer file sharing another good use for Merkle Trees, where we start by fetching the root of the tree from a trusted source to access a given file.
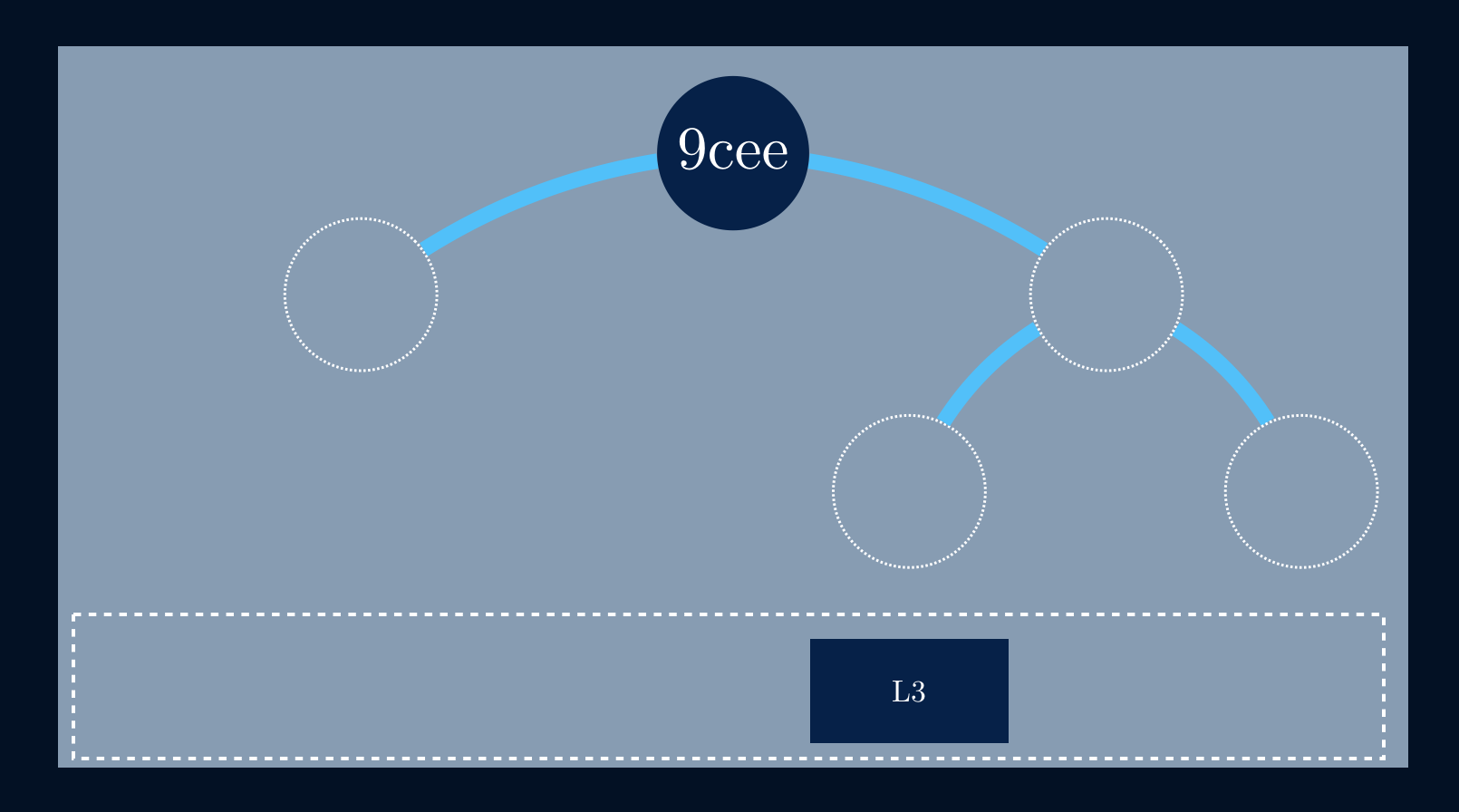
Since we can fetch single parts of a tree, reducing the amount of transferred data, we then fetch chunks of data from untrusted sources.
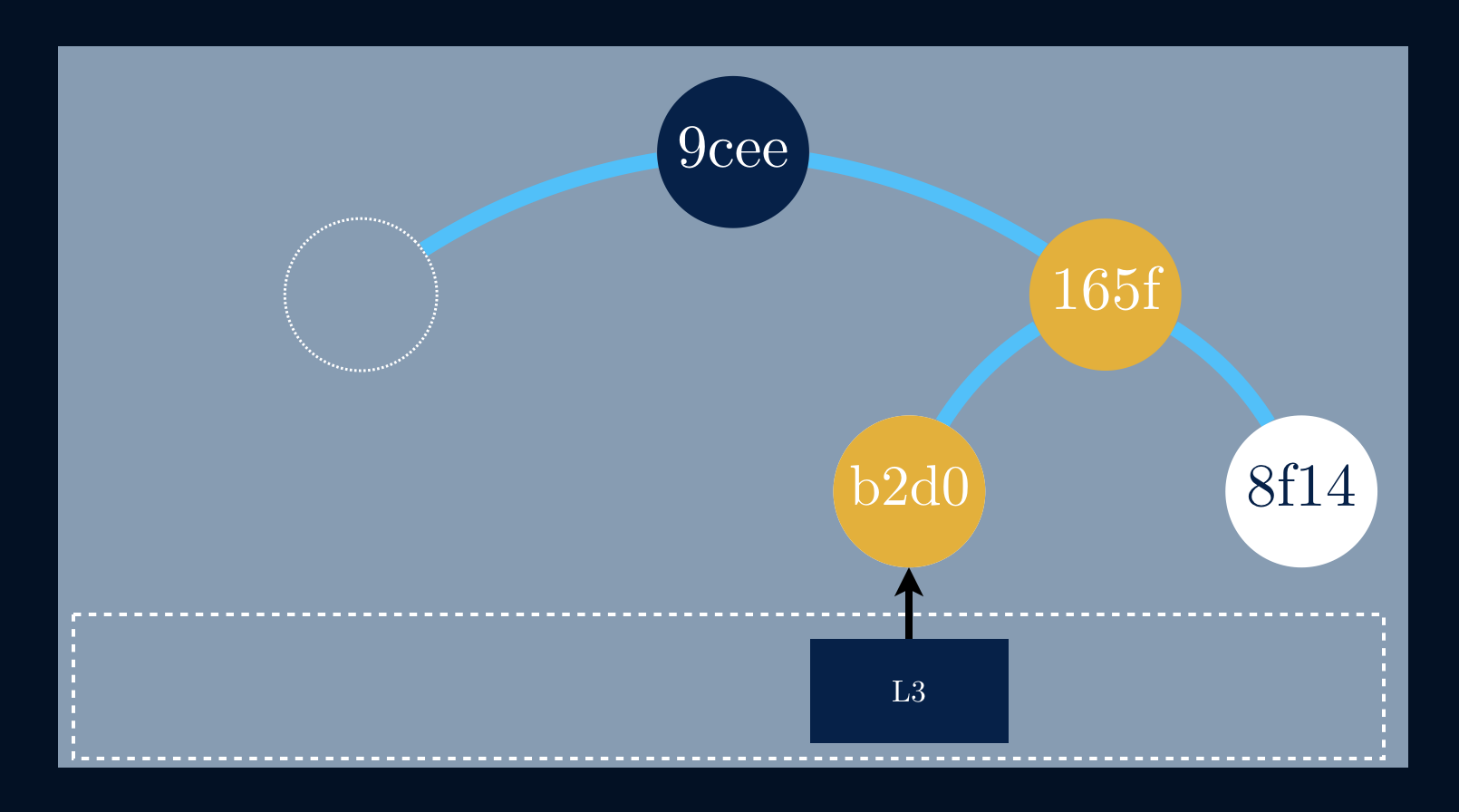
We start by fetching L3 and deriving its hash, b2d0. To allow us to get to
the root, we must fetch the hash value from the right leaf, 8f14. With these
two nodes, we can derive the next hash value, 165f. By fetching the last
hash, e831, we can use it, alongside with 165f, to derive the root hash,
which is indeed 9cee.
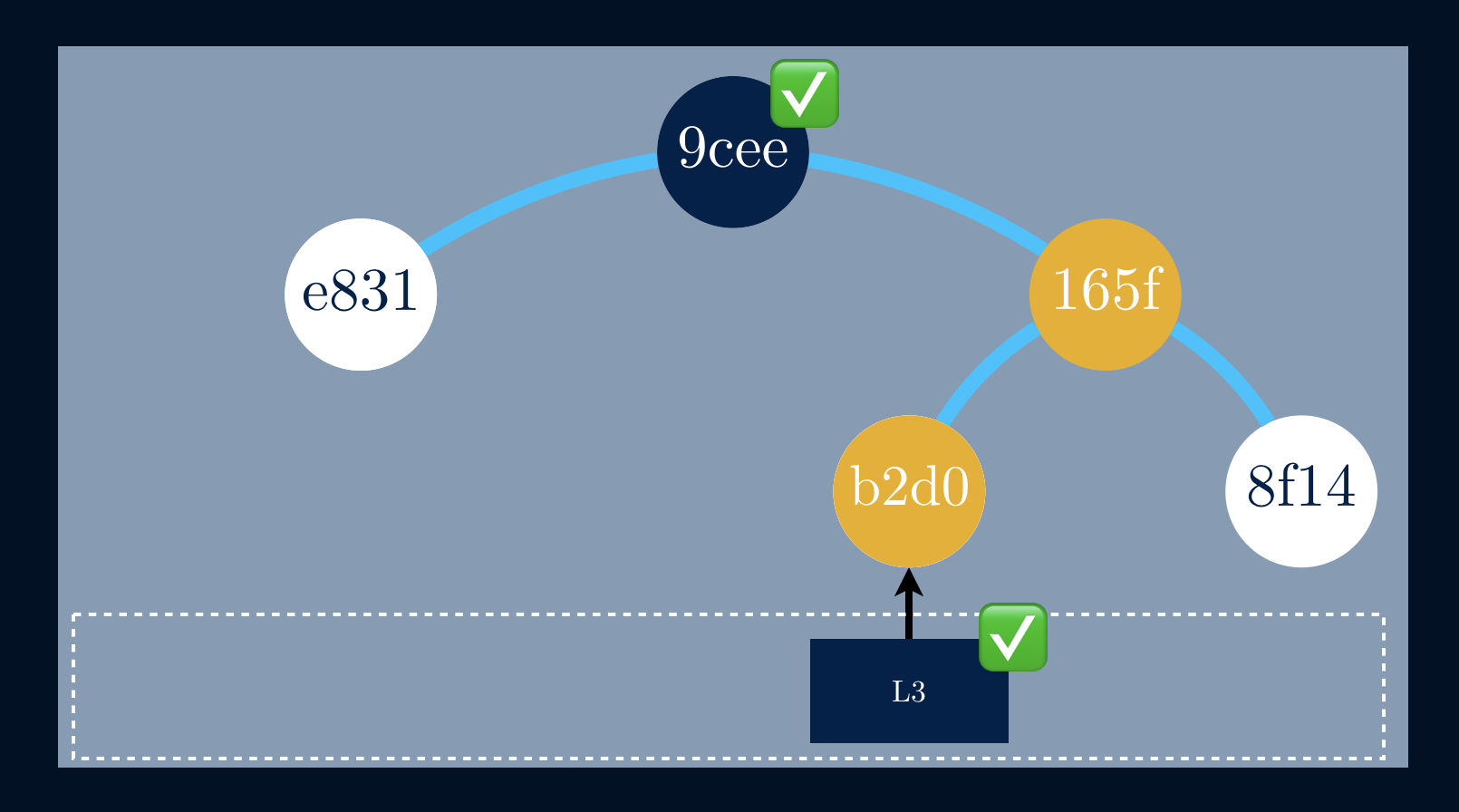
We were building a partial tree having just the root hash and a given data block. If the root computed from the audit path matches the true root, then the audit path is proof that the data block exists in the tree.
Copy-On-Write
Copy-on-write data structures are also called persistent data structures, since the old version is preserved. The idea is to share the same tree between both the copy and the original tree, instead of taking a full copy.
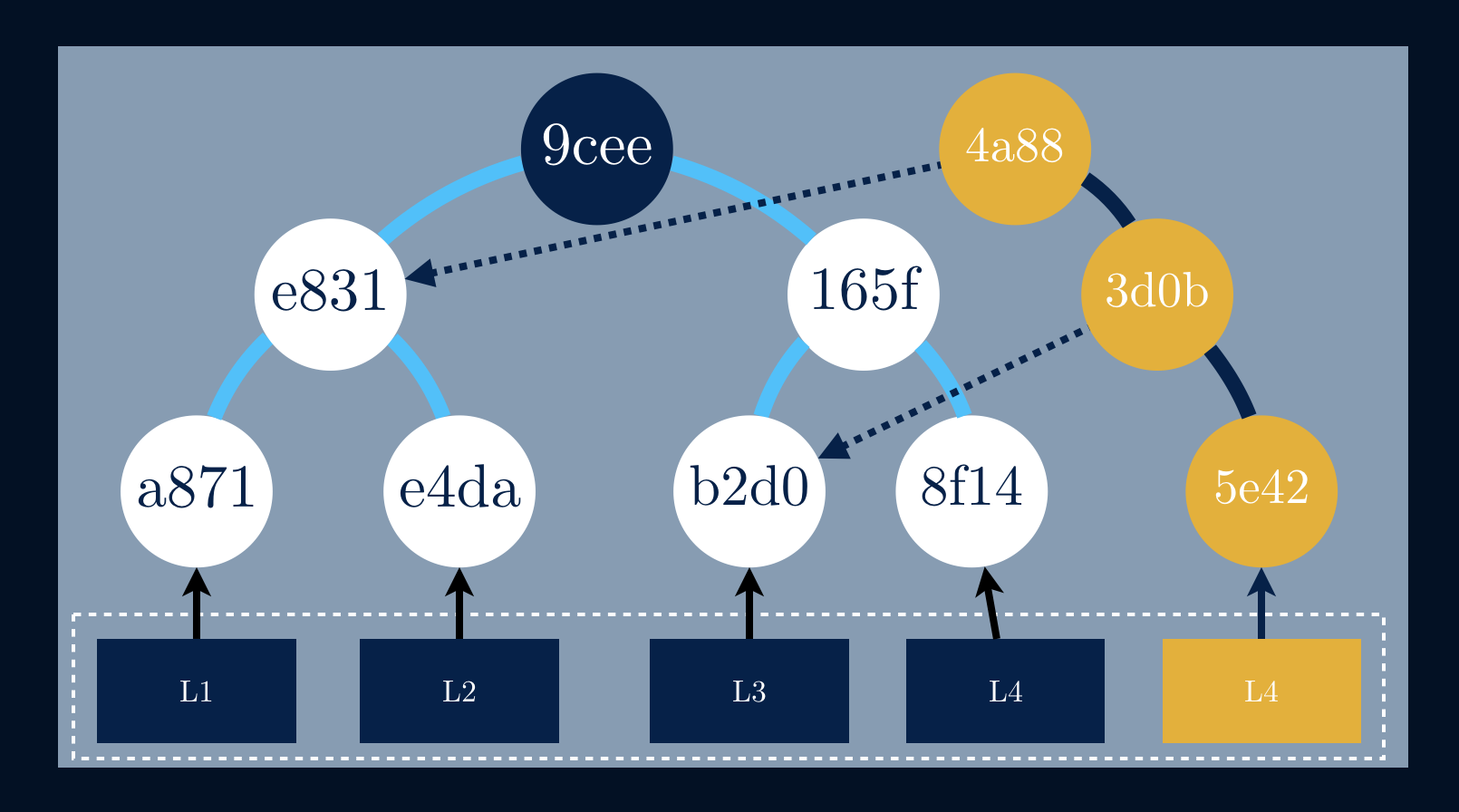
Having a given tree that suffers an update to a single data block L4, the
branch that links to it must calculate new hashes all the way up to the
root, although, the other branches stay intact.
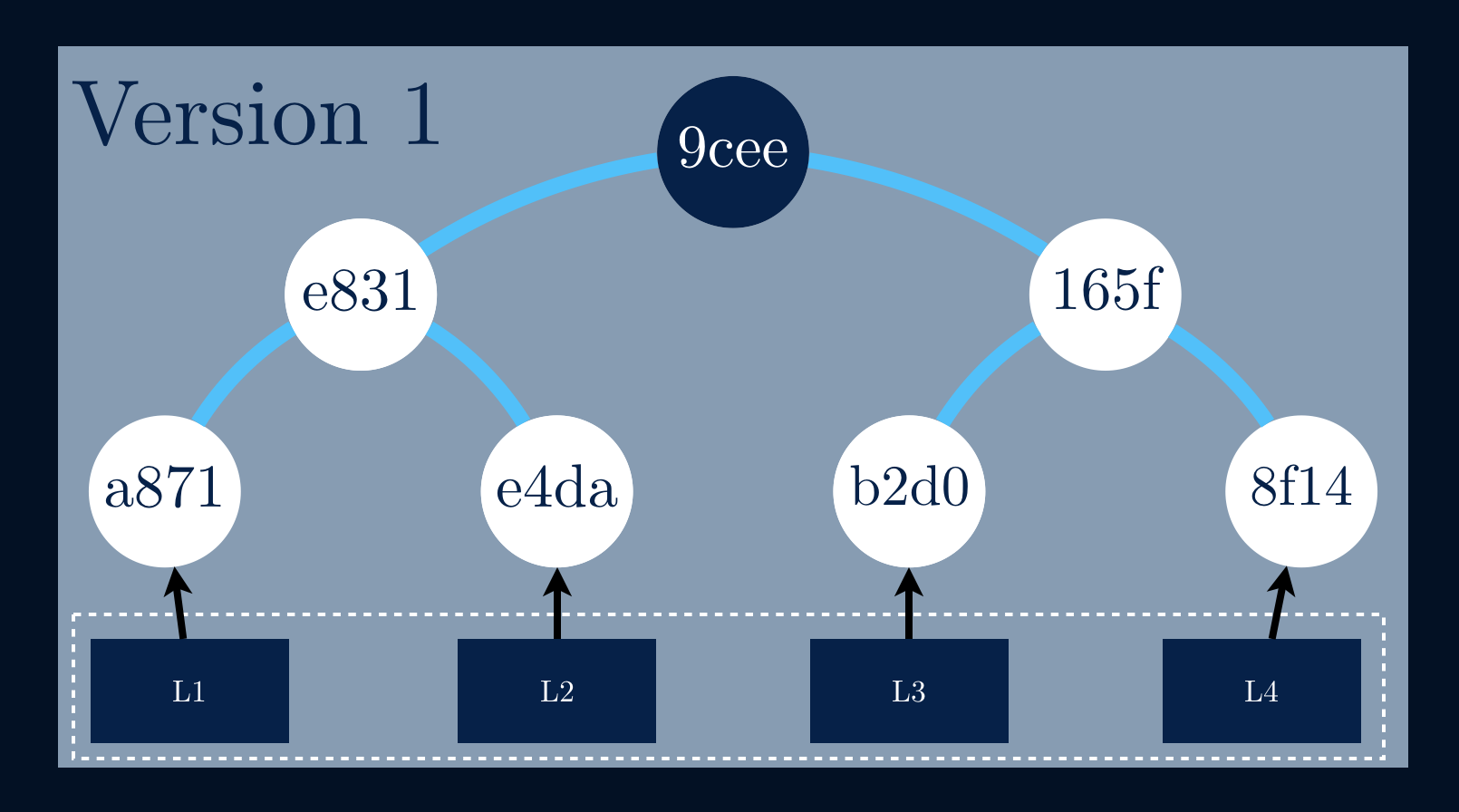
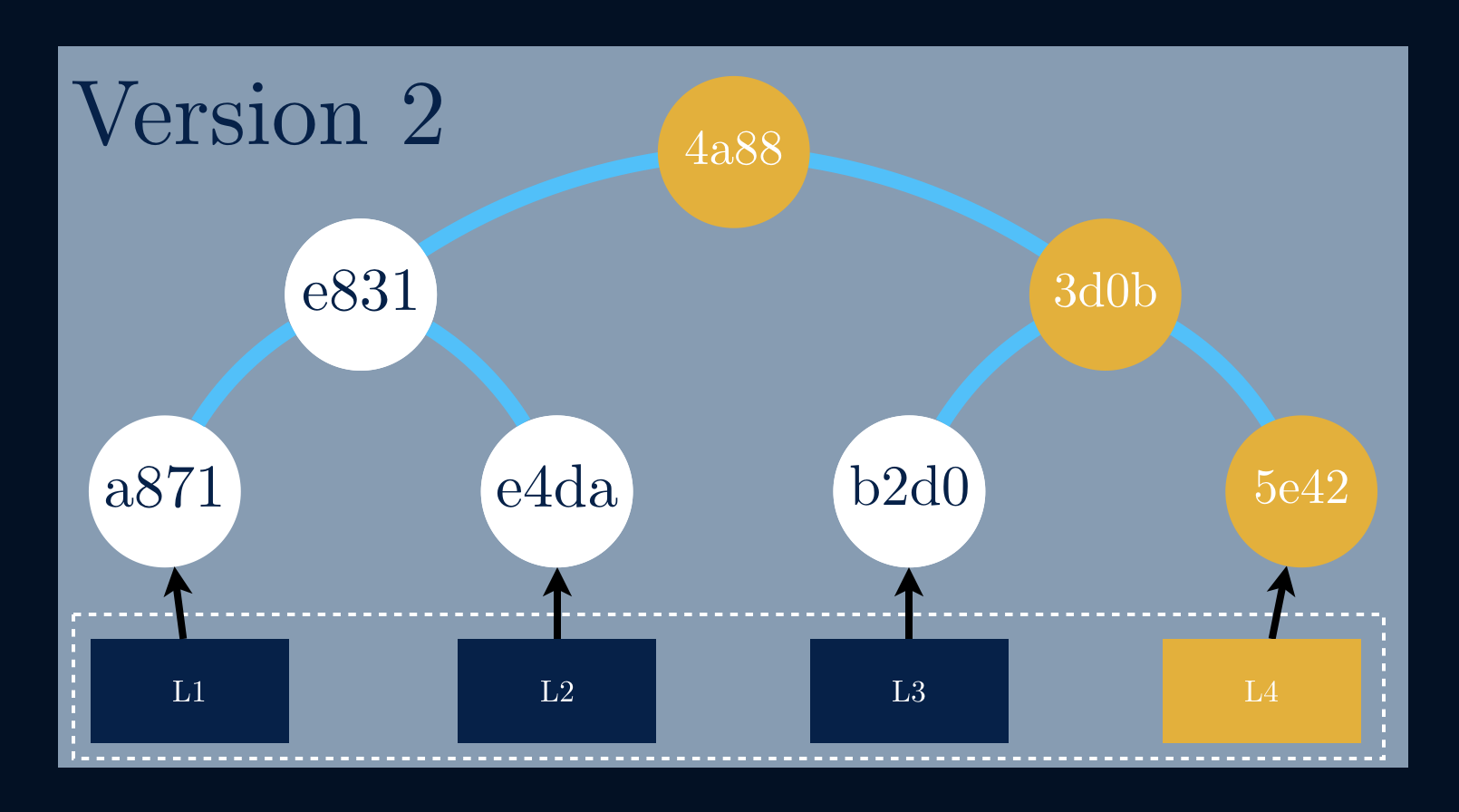
If we take a closer look we can see that we’re adding only a new data block and three new hashes for the new version of the data structure. All the other data blocks, eventually, gigabytes of data are being shared between both versions!
Wrapping up

Merkle trees are just binary trees containing an infinite number of cryptographic hashes where leaves contain hashes of data blocks and nodes contain hashes of their children. They also produce a Merkle Root that summarizes the entire data set and that’s publicly distributed across the network and can easily prove that a given data block exists in the tree.
You can find them in Cassandra, IPFS, Riak, Ethereum, Bitcoin, Open ZFS, and much more. Also, you have lots of papers to read as well if you want to dive even deeper.
Have fun!